excellent reading...enjoying while learning..subscribed
Carpe Diem
2
What is A book vs B book in Forex trading? 30 replies
A book forex brokers VS B book brokers, differences? 12 replies
Traders' Book Club 10 replies
The Book Club 5 replies

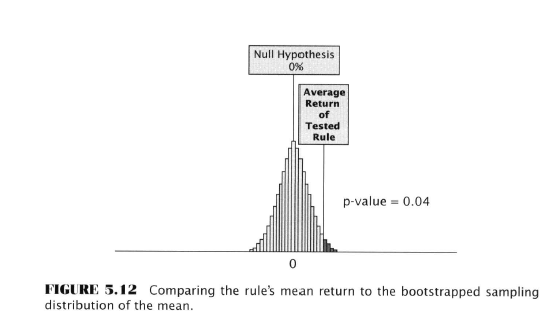

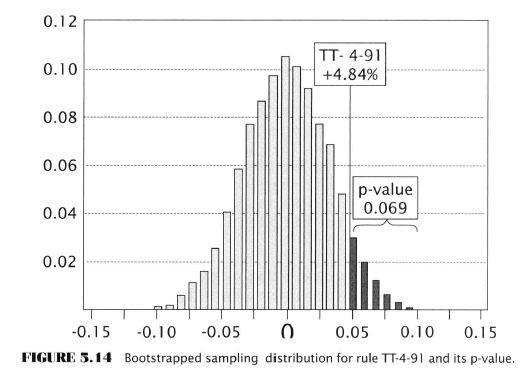
Possibly, like me you were champing at the bit to know what the actual rule is that we can use to make money, but not so fast partner, that’s all revealed in chapter 8, the next to last one. First we have to look at Estimation.

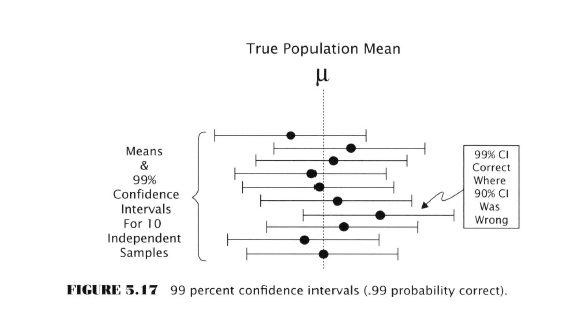




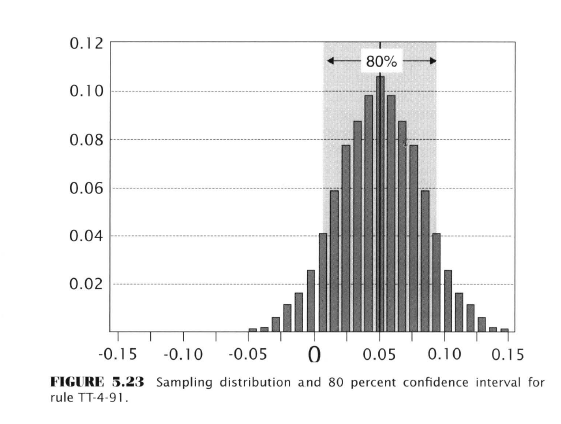
Falling Into the Pit: Tales of the Data-Mining Bias
The Problem of Erroneous Knowledge in Objective TA
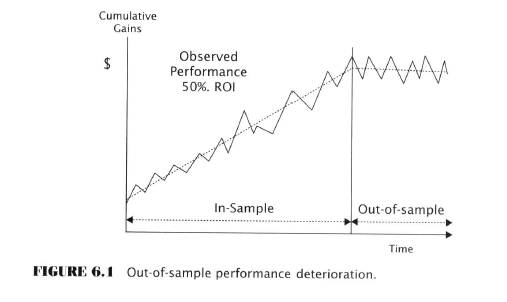
Data Mining
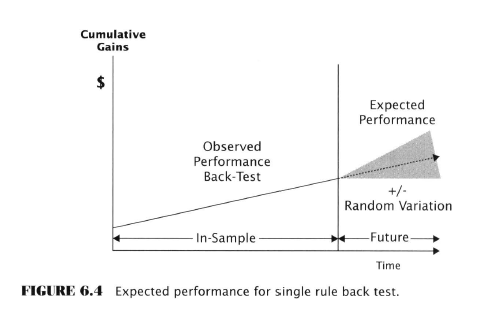
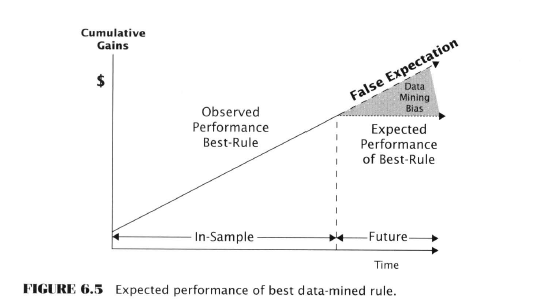
Data Mining and Statistical Inference
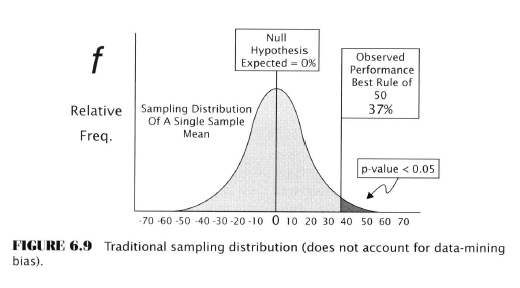
Significance Test Comparison
We have to do a little Ch. 5 recap to make this comparison but realize this first bit is about single-rule testing.
Now consider the case of the significance test for data mining:
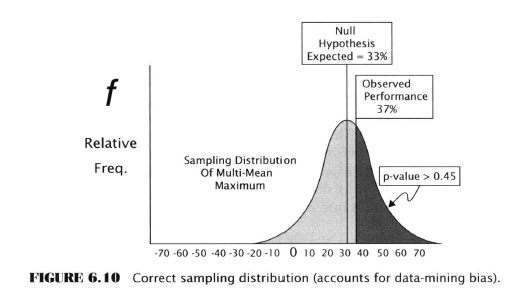
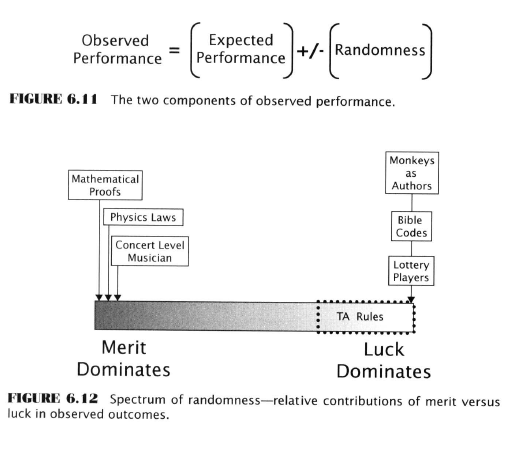

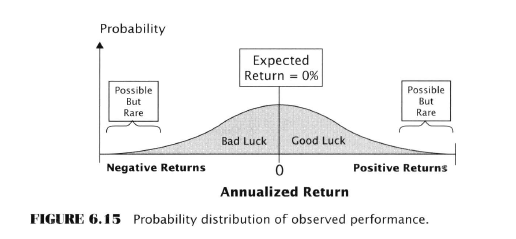
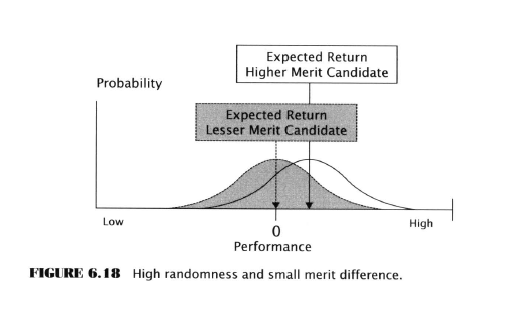
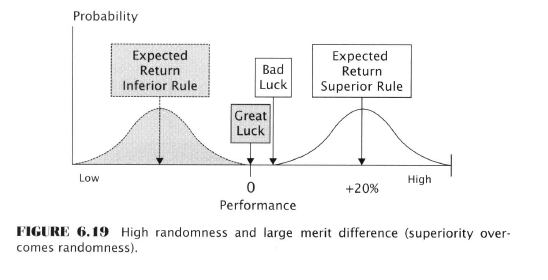
Five factors determine the magnitude of the Data-Mining Bias
Experimental Investigation of the Data-Mining Bias
Here Aronson embarks on several pages of experimental testing to investigate the effect of the above five factors on data-mining. He decides to use something called “artificial trading rules” because these can be controlled to know their true population parameters. Sounds fishy, but probably soothing to an academic mind.
He generates ATR performance histories using Monte Carlo methods. He then compares single rule backtests to MCP tests. He shows how the data-mining bias increases with the addition of more rules. He emphasizes the importance of sample sizes on the magnitude of bias. He examines the effects of rule correlation. He looks at distributions with fat and light tails
Maybe I’m getting lazy but this just seems like overkill. Of course, good science has to do this, but for our purposes, let’s just stipulate the professor is right. All we need to know then is what we’ve already read.



Aronson promised to put the software used for the MCP version on his website but I don’t see it. Some source code is in the Monte Carlo PDF.
The Importance of Theory
Scientific Theories
The Enemy’s Position: Efficient Markets and Random Walks

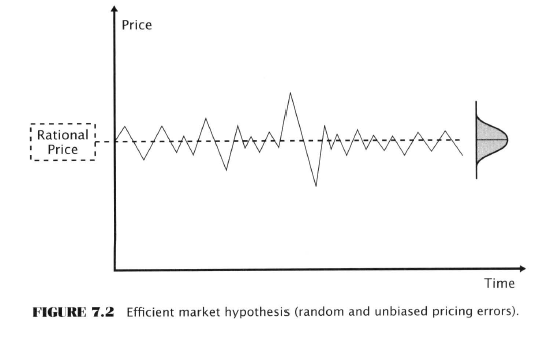


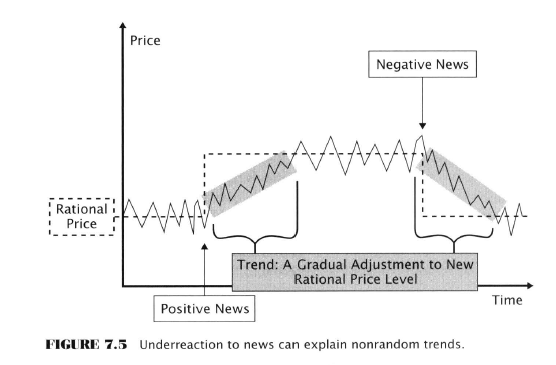
Next - Refuting the EMH!
Google Doc (footnotes - recommended for this chapter esp.)
I have to complain about why this idea is only being introduced now. This type of study would have been far more interesting than multiple appeals to the law of large numbers in previous chapters.
Next: Behavioral Finance : A Theory of Nonrandom Price Motion
Foundations of Behavioral Finance
BF rests on two foundational pillars:


Nonrandom Price Motion in the Context of Efficient Markets
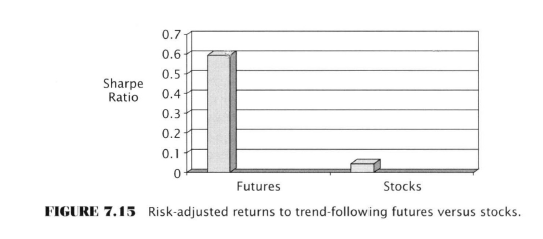
“Ultimately it is up to each method of TA to prove that it can [capture a portion of the nonrandom price behaviour].”
Data-Mining Bias and Rule Evaluation

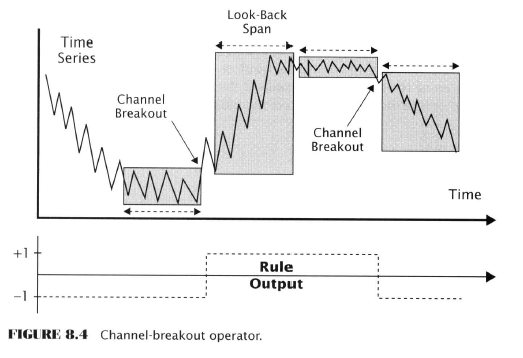



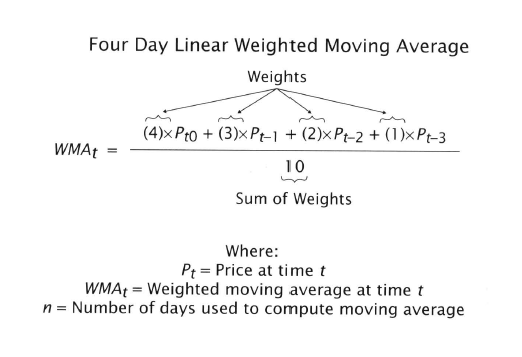

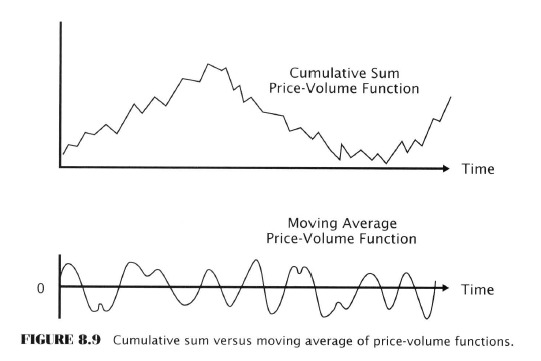





Market-Breadth Indicators


Interest-Rate-Spread Indicators
https://lh4.googleusercontent.com/9K...9mUB9Wr2ImfNkG
https://lh6.googleusercontent.com/J-...8PVfi1w-SO7-DN
https://lh3.googleusercontent.com/Vi...PfBxtoiHRCmawp
https://lh3.googleusercontent.com/fr...EGmuFSq6q-HpHo
https://lh6.googleusercontent.com/uS...CX-iT1lt2htNiQ
https://lh5.googleusercontent.com/SK...LFFZvhblHeyg8O
https://lh4.googleusercontent.com/07...HRQmw64-_wUePo
https://lh5.googleusercontent.com/Hk..._Njf2lqGJh2Zy1
The Rules



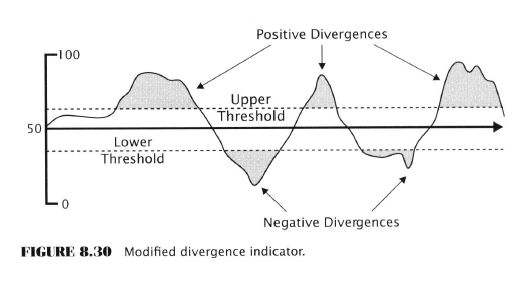
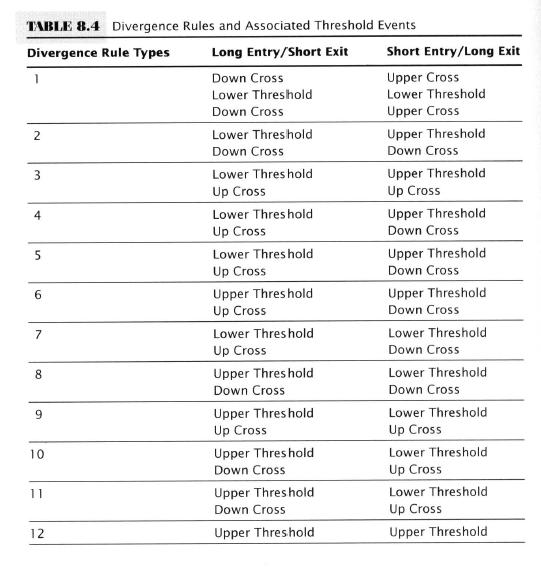

Just let this sink in for a second. After 9 chapters of dense slogging through academic-ese and with the aid of all the modern statistical and mathematical expertise available to a modern economist (ca. 2007 admittedly) at the end of it all Aronson comes up completely empty-handed with nothing to show for it!
“Oh I know what I can do to salvage this debacle. I’ll write a book.”
Good one, Aronson! Excellent joke. You had us going there for over 441 pages (so far)!
Dear reader, you can imagine how pissed off and disillusioned I was on first reading this admission of complete failure. Does that mean we have wasted our time? Well, no, as it turns out we have learned something (maybe a few things) even more valuable than a trading rule that might work for a few months and then mysteriously stop working. But let me save that for the end.
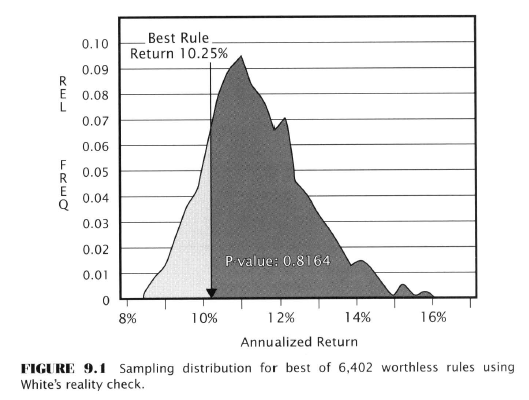
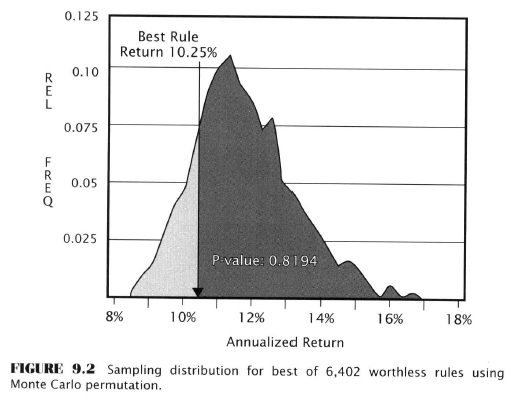
Critique (Aronson’s) of the Case Study
Positive Attributes
Negative attributes
Case Study Extensions


Next- what have we really learned, really?
Does this mean TA doesn’t work?
We haven’t proven it yet, but for me, it means we need to be humbler in our perceived ability to forecast future prices.
Think about it - I know you're really smart, but if a bunch of smart people like Aronson, Mandelbrot, Shannon, even Elder, Ehlers and the rest of the TA crew have tackled the problem of predicting market moves, and didn’t become billionaires (that we know about) and also just about every modern expert cannot do it (see my notes on FXStreet, ScorpionFX, Growth Aces, Patrick Munnelly, NoNonsenseFX, Huddleston, et al, for ex.) what chance do we have?
My opinion (which may change) is that it’s not hopeless, but I think we should move away from the ‘traditional’ technical analysis of Elliott/Gann/Fibonacci/periodic indicators and look at more exotic ideas like cyclical analysis (Hurst) and methods that don’t forecast. We haven’t even begun to delve into fundamental analysis yet, and we’ve barely scratched the surface of quantitative methods. So, there’s lots more to explore before we reach any ultimate conclusions.
-Before we abandon all traditional TA methods though let’s check out Al Brooks (modern candlestick patterns) but before that let’s read Reminiscences, which is not about TA but about good old fashioned trading ‘horse sense’ which might be the most important type of training of all
Overall their little experiment (which they caution does not meet any standard of rigour or scientific accuracy and may be subject to seasonality) shows that momentum (trends) continue with high reliability especially if our profit goals are modest. I think this is the kind of experiment that bears repeating.
This study convinced me that trading with fixed exits is superior to using trailing. It's also a good basis for trying out different exit strategies that can use a hybrid short-term/long-term move approach. This type of focused research is unfortunately fairly rare, and is rarely done by retail traders, though they should.
FXEngines also used to offer a backtester which would have been interesting to check out, but sadly I don't think you can get it anymore.