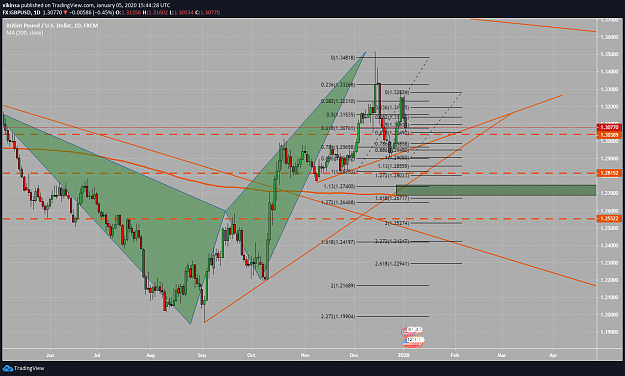
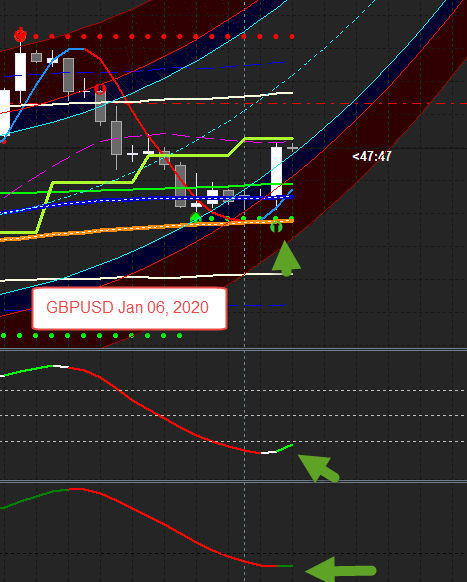
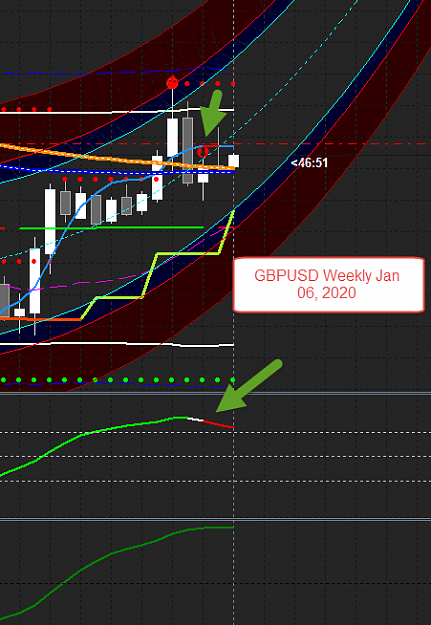
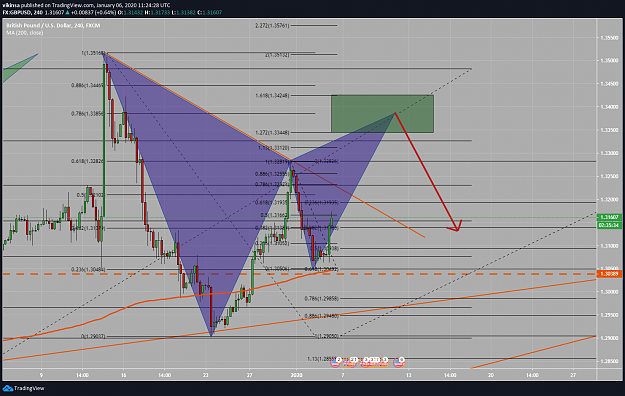
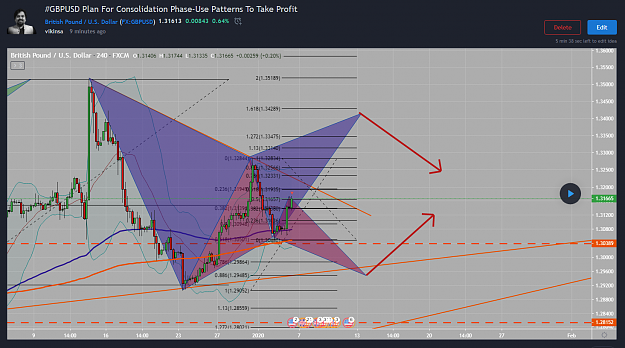
GBPUSD
All trades, systems, strategies are for my personal use only. I do not intend to give any kind of investment or financial advice of any sort. I use this thread only to log my analysis, planning, execution and results of trades. If you seek any value out of my posts, you are most welcome but please do so only educational purposes.
https://www.tradingview.com/u/vikinsa/
My Strategy Discussion: https://www.forexfactory.com/showthread.php?p=12678892
AUDUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970850
EURUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970846
GBPUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970847
USDCAD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970851
USDJPY Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970848
GOLD Trade Analysis Journal: https://www.metalsmine.com/showthread.php?t=971472
All trades, systems, strategies are for my personal use only. I do not intend to give any kind of investment or financial advice of any sort. I use this thread only to log my analysis, planning, execution and results of trades. If you seek any value out of my posts, you are most welcome but please do so only educational purposes.
https://www.tradingview.com/u/vikinsa/
My Strategy Discussion: https://www.forexfactory.com/showthread.php?p=12678892
AUDUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970850
EURUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970846
GBPUSD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970847
USDCAD Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970851
USDJPY Trade Analysis Journal: https://www.forexfactory.com/showthread.php?t=970848
GOLD Trade Analysis Journal: https://www.metalsmine.com/showthread.php?t=971472
Technical Analyst & Trader @ Vikinsa