Menu
Sister Sites

Options

Bookmark Thread

First Page First Unread Last Page Last Post

Print Thread

Similar Threads

Broker Challenge "NDD/STP" vs. True "ECN" and "Mkt Mkr" broker talk 46 replies

Time Frame Vs Personality, Which to choose as Main Time Frame? Who Are You? 10 replies

Importing and viewing indicators from other time frames on one chart (time frame) 4 replies

Time frame and Enter/Exit, Time frame and S/L, T/P relationships. 91 replies

Question on Lower Time Frame Indicators Vs. Longer Time Frame 7 replies

Attachments: Project Ultra - True "Other Time Frame" Indicators
Exit Attachments

Project Ultra - True "Other Time Frame" Indicators

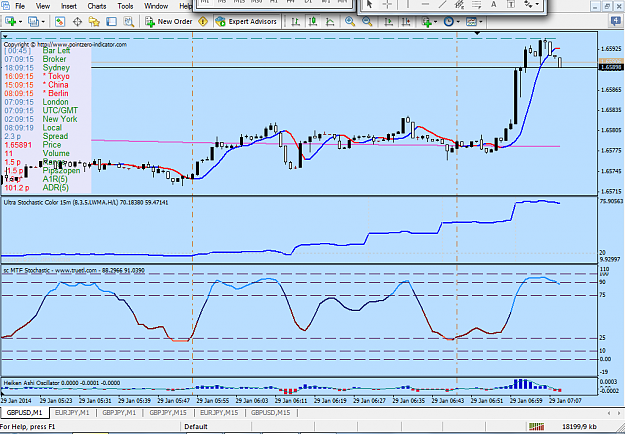
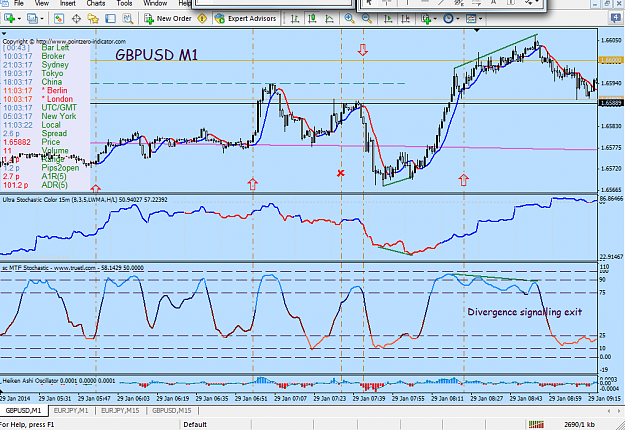
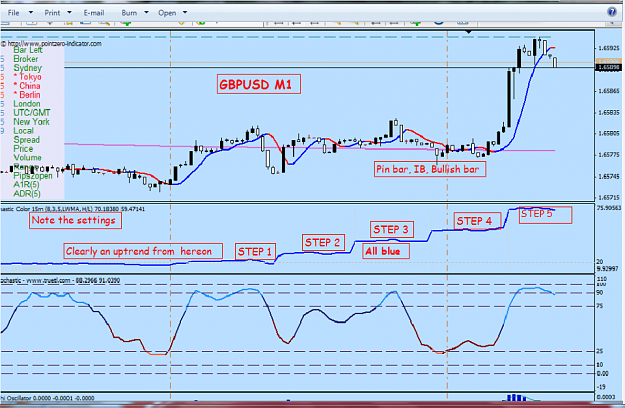
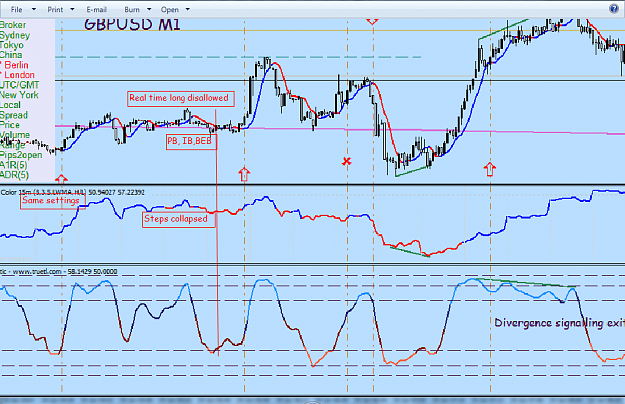
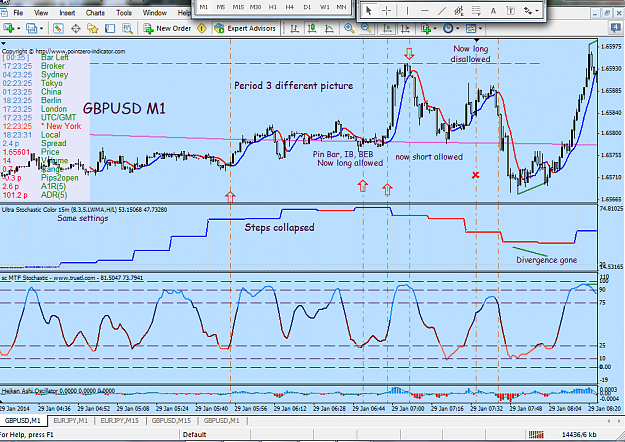
For some time I have wondered if fractals might be used to select the important samples in a price time series, thus giving a fractal time-base. I ran across this paper that argues that such a set exists and seems to have a way to find that set.

This paper by Turiel points to a way to select this set using fractal decomposition. I have a problem trying to translate it into code so that it might be tested. In particular I need a way to find the Hurst exponents for each sample, and then sort the samples by exponent. I think that Turiel is claiming that the set with the smallest exponent makes up the most important set.

Anyone have any ideas?
Attached File(s)
File Type: zip Multi Fractal Geometry.zip   1.0 MB | 1,393 downloads
Thank you JMW1970 for the hard work - it looks very rewarding
Quoting jmw1970
[size=5]Project Ultra

[size=3][font=Arial]I have been working on providing true "other time frame" indicators (sometimes referred to as MTF indicators).

Traditionally these indicators simply get the final value of the corresponding bar in the other time frame and show this value, this leads to "step" effect, and in addition does not show you at detailed level how the value came to be. (an example is shown below)

The working name I gave to this project was "Project Ultra".

All indicators will be prefixed with the name !Ultra, the...
Hi,

Great work with these indis. Was just wondering if anyone could tell me what the traditional OTF/MTF indi is in the first post. I like the way it looks so trying to track it down.

Thanks for the work John.
Hi jmw1970,
i've found this macd zerolag indi that is great but it sucks a lot of cpu, could you please take a look at it and see if you can fix that issue?
Many thks
Attached File(s)
File Type: mq4 Zerolag MACD - alerts & arrows.mq4   12 KB | 1,093 downloads
Quoting strongtrader
Hi jmw1970,
i've found this macd zerolag indi that is great but it sucks a lot of cpu, could you please take a look at it and see if you can fix that issue?
Many thks
If it can help i've found this error message in my advisor tab:
invalid integer number as parameter 2 for iSeries function
Hi jmw1970

Thanks for sharing your MTF indicators.
I have tried the Stochastic and it seems to work fine but gives error messages in the Experts tab every about every tick. The message is:

2011.11.17 12:03:52 !Ultra Stochastic EURUSDm,M15: unknown subwindow number -1 for ObjectCreate function

Would appreciate a fix!

Regards
Success is a marathon, not a sprint!
jmw1970, it´s possible an ultra HA version?
thanks in advance.
Humble & Kalcker CLO2 = Covid killer
Hi jmw1970,

I really like your Ultra RSI and I must say that You saved me a lot of work providing this indicator.
Unfortunately when I change parameters to display info from Weekly timeframe all I can see is empty indicator window
All other timeframes are displayed correctly.
Can You fix this issue and upload corrected version ?

I’m using MT4 build 409 on VISTA 64bit Home Premium (if this will help you).

Best Regards
nht
[quote=jmw1970;4711139]Standard stochastic indicator with colored lines (up/down) with true OTF/MTF functionality. NOTE: The lines are colored up/down based not on the previous bar of the chart timeframe, but based on the previous bar of the "other" time frame so although the stochastic line is rising it could still be colored for falling because it is still below the previous other timeframes final value {file} {image}[/QUOTE

jmw1970

very useful indicator,
but I can not install on my MT4, can give me an idea?
thank you and sorry my language is bad ..
Quoting jmw1970
Standard stochastic indicator with colored lines (up/down) with true OTF/MTF functionality. NOTE: The lines are colored up/down based not on the previous bar of the chart timeframe, but based on the previous bar of the "other" time frame so although the stochastic line is rising it could still be colored for falling because it is still below the previous other timeframes final value {file} {image}
Hello JW,

Great work you've done here, I love the way the OTF Stoch with colour lines gives clear signals, very helpful.
However I tried the indicator and monitored it in real time and I found it repaints more than is allowable for traditional MTF indicators, it repaints whole periods and repaints same repainted periods some more.
Ideally once a higher time frame candle closes, that period repainting ends, but this is not the case with this indicator.
In real time you get great signals but afterwards those signal change and change.
I'm sure you can amend this little glitch and revise the code, take a look at what I'm talking about, see the sequence of the 1st two screen shots and the closer look of the 3 following screen shots, they prove my point.
Attached Image(s) (click to enlarge)
Click to Enlarge Name: WHAT A MISS.png Size: 85 KB
Click to Enlarge Name: CABLE ACTION.png Size: 92 KB
Click to Enlarge Name: PERIOD 1.png Size: 157 KB
Click to Enlarge Name: PERIOD 2.png Size: 84 KB
Click to Enlarge Name: Period 3.png Size: 118 KB
Let it turn and find your entry.
Please is there any ultra macd?
Quoting grugged
Please is there any ultra macd?
It's already 3 years since he last posted here..
hi
to ultra project.
i use it and many thanks bout that.
my problem:
when i want to call indicator with icustom function i will receive below error
UltraRSI: unknown subwindow number -1 for object create function.
//---
i think my code is correct and this problem about UlraRSI.ex4 file.
//---
can anybody help me about this problem?
many thanks
With this sort of indicators, it's possible to backtest MTF with MT4, easy to find the cross of an indicator and his signal at x 1mn candles.
I have coded 14 MTF indicators.
On this sample screenshot, EMA day 1h, BBand 1h, Stochastic+signal 1h, Trix+Signal 1h, RSI 1h, MACD 1h, KST 1h.
Attached Image (click to enlarge)
Click to Enlarge Name: Screenshot2.png Size: 124 KB
Trade Less, trade Better, trade True MTF!
Are any of these indicators still being developed? Would be great to have the option for a working weekly setting on the Ultra Stochastic. These are great indicators by the way.
A fool learns from his mistakes. A wise man learns from the fools mistakes.
  • Post #56
  • Quote
  • Last Post: Dec 28, 2020 10:46pm Dec 28, 2020 10:46pm
would you please give me this indicator for mt5. Bro I use MT5 so please can you make this indicator for mt5. please.
0 traders viewing now