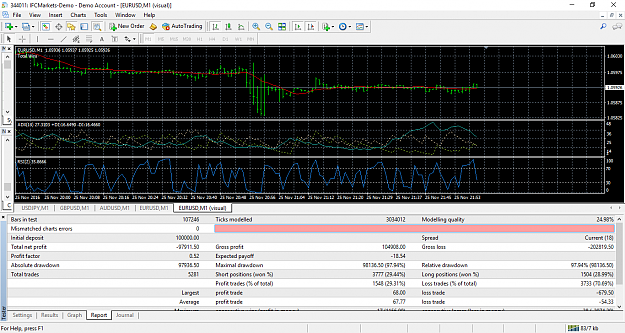
Hello, I am working on a EA based on a strategy developed by Brandon Williams for 5 minute binary options on nadex. I am new to coding in MQL4 so the strategy I built is not that good and might not even follow Brandon strategy as of right now. Therefore, I decided share this strategy hoping we can improve it.
See strategy here
https://vimeo.com/218865665
will share password only if you agree to share results of EA by becoming a tester or coder
newest EA is posted to test out in the thread
Developers/Coders
1. Beerbelly
2. ADance
Testers
1. samirrad
2. charli86
See strategy here
https://vimeo.com/218865665
will share password only if you agree to share results of EA by becoming a tester or coder
newest EA is posted to test out in the thread
Developers/Coders
1. Beerbelly
2. ADance
Testers
1. samirrad
2. charli86