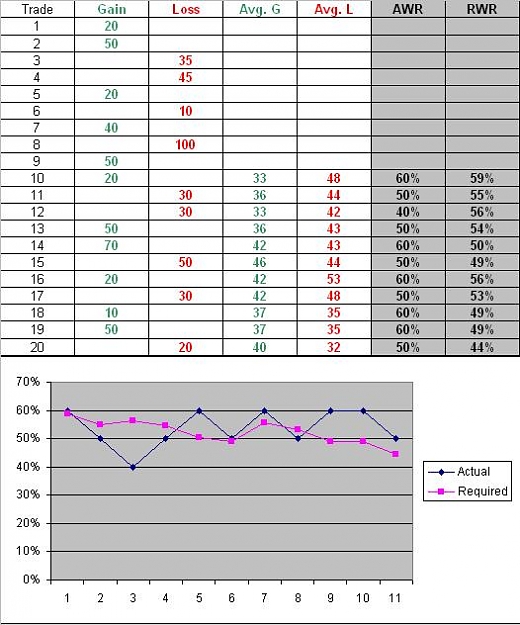
Actually, without some definite edge, expectancy is always negative because of spreads and commissions. Here's why.
Most traders will be familiar with the standard expectancy equation:
W = win rate
G = average Gain (or predefined TP if there is one)
L = average Loss (or predefined SL point if there is one)
Expectancy = WG - (1-W)L
This is like trading math 101 but it is very compelling to new traders who think that it is the key to sure consistent success. "After all," they think, "if I just cut my losses to 10 pips, and let my trades run to 30 pips, then even if I only win 30% of the time then I would still be ahead!"
That is of course because (0.30 x 30) - (0.70 x 10) = 9 - 7 = 2 pips/trade.
Wow! Any dolt can be right only 30% of the time, so all I have to do is make a million trades this year and I'll be up 2 million pips! Right? Right????
Ummm, no. :
:
Let's get beyond trading math 101 to the next step. What's wrong with the train of thought above is that the win rate is actually a function of your risk/reward ratio.
Suppose you set your stop at 1 pip and your TP at 800 pips on every trade. How many do you think you'd win? Your win rate would be virtually zero. Now if you reversed the situation and set your TP at 1 pip and your stop at 800 pips then your win rate would be very close to 100% If your SL and TP are at the same distance from your entry, then your win rate should be about 50%. In fact, your win rate (all else being equal) should be equal to the distance to the stop divided by the total distance from the stop to the target.
For example if your SL is 20 pips from entry and your TP is 80 pips from entry, then your win rate on trades like that should be around 20%. If you set a stop at 20 pips and a TP at 5 pips then your win rate should be about
20 / (20 + 5) = 20/25 = 80%
So I'm saying that in terms of the variables in the standard "expectancy" equation, the win rate is actually equal to: L / (L+G)
So let's plug that into the expectancy equation and see what we get shall we? We started with:
E = WG - (1-W)L
but now we know that W = L / (L+G) so...
E = LG / (L+G) - L + L^2 / (L+G) note: L^ is "L squared."
multiplying the middle term on the right by (L+G)/(L+G) which is just 1:
E = LG / (L+G) - L(L+G) / (L+G) + L^2 / (L+G)
combining into one fraction with a common denominator:
E = (LG - L(L+G) + L^2) / (L+G)
E = (LG - L^2 - LG + L^2) / (L+G)
E= 0 / (L+G)
E = 0
And that in a nutshell is why trading can be difficult. Just depending on old pat bromides like "cut your losses short and let your profits run," or "you can't go broke taking profits," although they sound good will not really get you anywhere.
Sure, if you cut your losses short, you know what you get? A lot of little losses which just about equal your very infrequent big wins. If you follow the opposite advice that "you can't go broke taking profits," and decide to use wide stops and tight targets guess what? You get a lot of little profits that just about make up for that huge loss you take every so often.
All of these cute slogans do nothing more than represent different points along the risk/reward spectrum, but traders should be aware that each of those points has an expectancy of about zero. And that's not including costs. So forget the cute slogans. The key to trading successfully is to find an edge that moves that E value slightly to the positive side of your costs.
Most traders will be familiar with the standard expectancy equation:
W = win rate
G = average Gain (or predefined TP if there is one)
L = average Loss (or predefined SL point if there is one)
Expectancy = WG - (1-W)L
This is like trading math 101 but it is very compelling to new traders who think that it is the key to sure consistent success. "After all," they think, "if I just cut my losses to 10 pips, and let my trades run to 30 pips, then even if I only win 30% of the time then I would still be ahead!"
That is of course because (0.30 x 30) - (0.70 x 10) = 9 - 7 = 2 pips/trade.
Wow! Any dolt can be right only 30% of the time, so all I have to do is make a million trades this year and I'll be up 2 million pips! Right? Right????
Ummm, no.
Let's get beyond trading math 101 to the next step. What's wrong with the train of thought above is that the win rate is actually a function of your risk/reward ratio.
Suppose you set your stop at 1 pip and your TP at 800 pips on every trade. How many do you think you'd win? Your win rate would be virtually zero. Now if you reversed the situation and set your TP at 1 pip and your stop at 800 pips then your win rate would be very close to 100% If your SL and TP are at the same distance from your entry, then your win rate should be about 50%. In fact, your win rate (all else being equal) should be equal to the distance to the stop divided by the total distance from the stop to the target.
For example if your SL is 20 pips from entry and your TP is 80 pips from entry, then your win rate on trades like that should be around 20%. If you set a stop at 20 pips and a TP at 5 pips then your win rate should be about
20 / (20 + 5) = 20/25 = 80%
So I'm saying that in terms of the variables in the standard "expectancy" equation, the win rate is actually equal to: L / (L+G)
So let's plug that into the expectancy equation and see what we get shall we? We started with:
E = WG - (1-W)L
but now we know that W = L / (L+G) so...
E = LG / (L+G) - L + L^2 / (L+G) note: L^ is "L squared."
multiplying the middle term on the right by (L+G)/(L+G) which is just 1:
E = LG / (L+G) - L(L+G) / (L+G) + L^2 / (L+G)
combining into one fraction with a common denominator:
E = (LG - L(L+G) + L^2) / (L+G)
E = (LG - L^2 - LG + L^2) / (L+G)
E= 0 / (L+G)
E = 0
And that in a nutshell is why trading can be difficult. Just depending on old pat bromides like "cut your losses short and let your profits run," or "you can't go broke taking profits," although they sound good will not really get you anywhere.
Sure, if you cut your losses short, you know what you get? A lot of little losses which just about equal your very infrequent big wins. If you follow the opposite advice that "you can't go broke taking profits," and decide to use wide stops and tight targets guess what? You get a lot of little profits that just about make up for that huge loss you take every so often.
All of these cute slogans do nothing more than represent different points along the risk/reward spectrum, but traders should be aware that each of those points has an expectancy of about zero. And that's not including costs. So forget the cute slogans. The key to trading successfully is to find an edge that moves that E value slightly to the positive side of your costs.