- Post #22,521
- Quote
- Dec 11, 2013 7:23am Dec 11, 2013 7:23am
- Joined Oct 2007 | Status: Sniper | 14,763 Posts
- Post #22,524
- Quote
- Dec 11, 2013 12:18pm Dec 11, 2013 12:18pm
- | Joined Jul 2012 | Status: consciuos incompetence level | 2,064 Posts
JacekPreserve Precious Capital
- Post #22,525
- Quote
- Dec 11, 2013 12:29pm Dec 11, 2013 12:29pm
- | Joined Jul 2012 | Status: consciuos incompetence level | 2,064 Posts
JacekPreserve Precious Capital
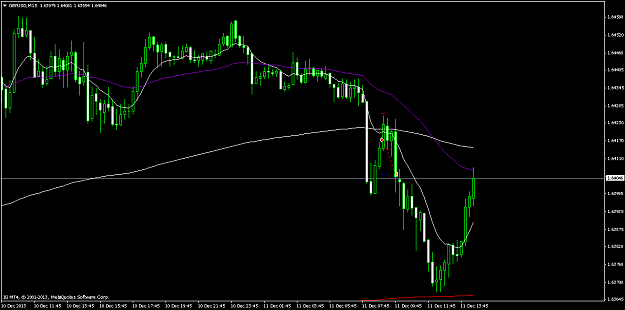
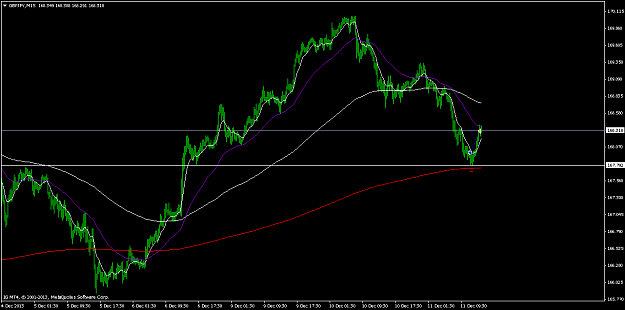
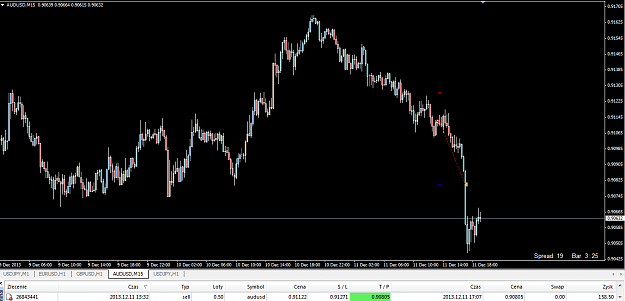
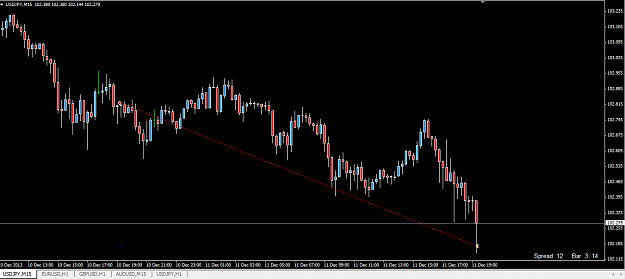
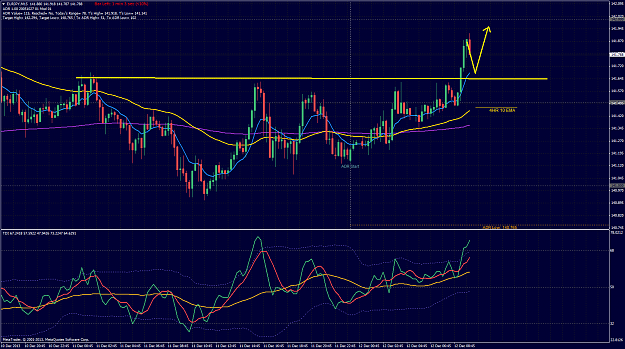
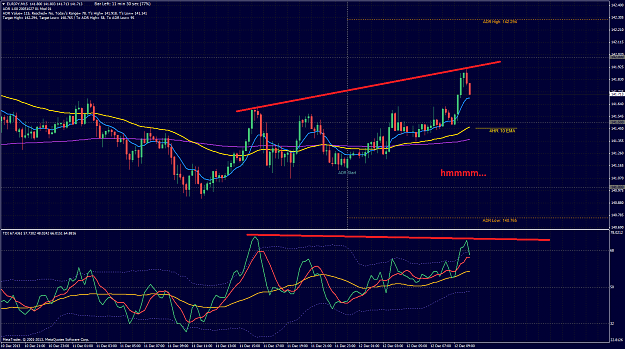
![Click to Enlarge
Name: 2013-12-12 10_26_10-81488146_ FXCM MetaTrader 4 - Compte Démo - [EURUSD,M15].png
Size: 65 KB](/attachment/image/1328958/thumbnail?d=1386844193)
![Click to Enlarge
Name: 2013-12-12 10_31_27-81488146_ FXCM MetaTrader 4 - Compte Démo - [GBPUSD,M15].png
Size: 66 KB](/attachment/image/1328961/thumbnail?d=1386844439)
![Click to Enlarge
Name: 2013-12-12 10_34_54-81488146_ FXCM MetaTrader 4 - Compte Démo - [GBPJPY,M5].png
Size: 57 KB](/attachment/image/1328962/thumbnail?d=1386844613)