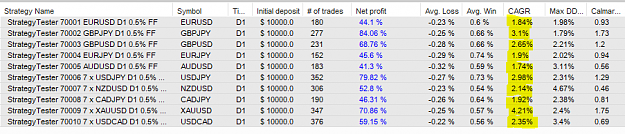
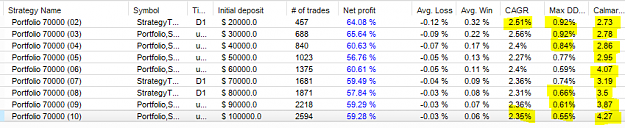
(credit to Thomas Hollands for the summary)
On Time and Risk: Brilliant essay by @ole_b_peters. Some takeaways.
The game: You roll a die. If a 6, I give you 100x your wealth. If not, you give me everything you own. The expected return is 1600%. Should you play?
On Time and Risk: Brilliant essay by @ole_b_peters. Some takeaways.
The game: You roll a die. If a 6, I give you 100x your wealth. If not, you give me everything you own. The expected return is 1600%. Should you play?
- The maths seem to suggest it is rational to play. But that's because we're used to calculating ensemble averages.
- An ensemble average is taken over many games simultaneously - in imagined parallel universes. A time average is taken as you play each game one after the next. Time averages =/= ensemble averages for most real systems.
- In real life, you can only play each game one after the next. And at each game your probability of ruin is 5/6. It is easy to see if you play multiple times, p(ruin) -> 1
- The tools of stat physics were developed on ergodic systems, for which ensemble and time averages are equal. In real systems we cannot substitute them and must be careful. Poor risk management in the financial crisis stemmed in part from this error.
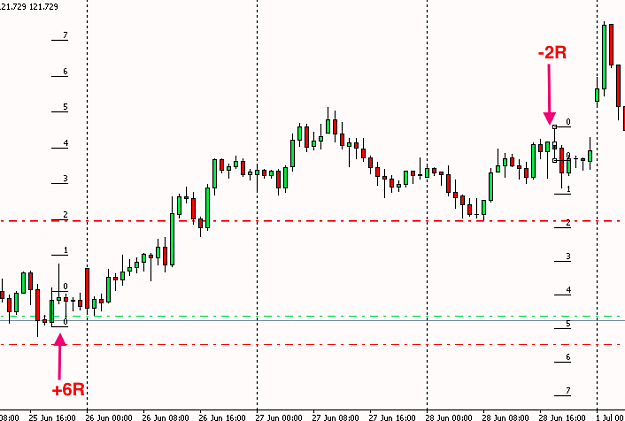
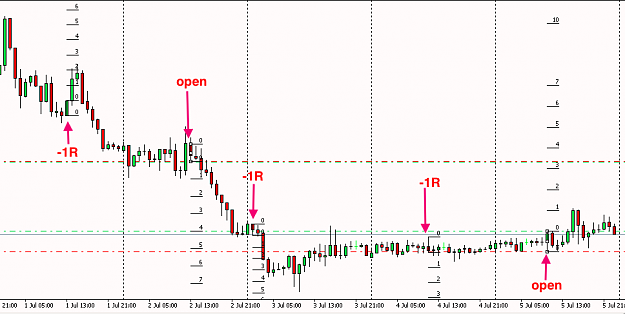
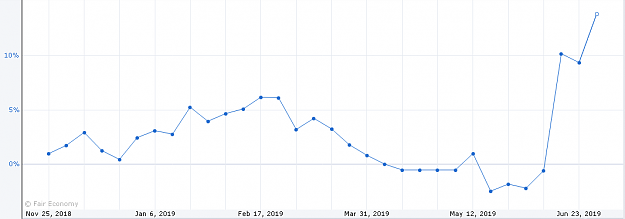
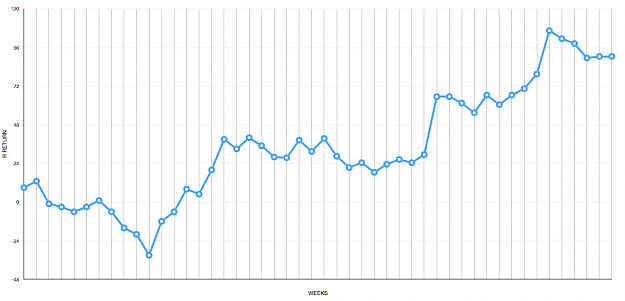
- The game is so risky because all your wealth is on the line. If you instead bet a fraction of your wealth, p(ruin) quickly goes to 0, while your potential upside stays high.
- How can we use this in real life? Take bets for which p(ruin) -> 0, but the ensemble expected return is high. High potential for upside, while ensuring you stay in the game.
tradewith60
3